Calculatrice brouillon

Dans ce type d'utilisation de la calculatrice, les élèves la considèrent comme un outil local de création ; dans certains cas, c'est la seule propriété de la calculatrice qui est publiquement déclarée comme utile ; dans ce qui suit, je m'appuie sur une observation et un entretien lors de l'épreuve pratique de mathématiques dans le lycée A ; le sujet tiré au sort par G1 ainsi que l'observation sont détaillés en annexe obs19mai ; le sujet propose le calcul de :

$$\lim_{n \to \infty}\int_0^1\left(1+\frac{x}{n}\right)^n dx$$

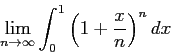
Lors de l'entretien, G1 déclare :

G1 : Ben, c'est vrai que c'est pratique pour les, les, les représentations graphiques. Après, pour tout ce qui est calcul, moi, je préfère faire les calculs à  la main, donc ça m'aide pas vraiment en dehors des représentations...

[...]

O : D'accord, et vous travaillez avec la calculatrice, alors ?

G1 : Ouais, mais, je l'utilise pas tant que ça...

O : Vous ne l'utilisez pas tant que ça, mais quand vous l'utilisez, vous l'utilisez comment ?

G1 : Pour faire les dérivées,..., quelques intégrales, pour vérifier, c'est tout,...mais c'est pas pour euhh

Annexe entretien19mai

Pour cet élève, les propriétés de stockage ou de communication ne sont apparemment pas utilisées ; pourtant, un peu plus tard :

O : Et alors, pour le bac, vous pensez que la calculatrice peut vous apporter quelque chose ?

G1 : Ah oui, oui, c'est sûr, c'est un gros atout pour le bac.

O : A quel niveau ?

G1 : Ben ça évite,...c'est rassurant d'avoir des démonstrations, parce qu'on en a beaucoup, puis on peut vérifier tous nos calculs...

Annexe entretien19mai

Il s'agit d'apparent paradoxe que l'analyse du travail de G1 lors de l'épreuve pratique (Annexe obs19mai) en utilisant une analyse des incidents didactiques permet de lever :

Dans un premier épisode, G1 trace la représentation graphique de la fonction $fn : x \longmapsto \left(1+\frac{x}{n}\right)^n$ et dirige la valeur de $n$ en utilisant un curseur dont il règle la valeur maximale à $10^6$. De fait, graphiquement, la fonction représentée est proche de l'exponentielle, ce qui permet à G1 de répondre correctement à l'examinateur. La valeur maximum de $n$ est cependant créatrice d'un incident de syntaxe dans le troisième épisode.

Dans le deuxième épisode, un incident de contrat est provoqué par l'examinateur qui veut diriger l'élève vers une interprétation géométrique de l'intégrale ; alors que G1 commençait à calculer la valeur exacte de l'intégrale de $fn$ sur $[0,1]$, l'examinateur suggère de représenter graphiquement cette intégrale ce qui provoque l'incident de syntaxe et la perturbation suivante.

Dans le troisième épisode, après avoir demandé la représentation graphique de l'aire et son calcul approché avec la valeur $n=10^6$, le logiciel affiche 0. Devant cette rétroaction surprenante et paradoxale, G1 annule ses manipulations ; aux yeux de l'examinateur qui n'a pas été témoin de cette phase, il semble ne pas comprendre l'interprétation graphique de l'intégrale :

P : Qu'est ce que tu cherches à  faire ? .

Après quelques instants de discussion, l'examinateur demande à l'élève de modifier cette valeur maximale de $n$ et de travailler avec des valeurs  plus raisonnables . 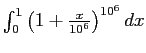Il y a évidemment une contradiction entre le fonctionnement du logiciel dans le registre graphique (le logiciel représente la fonction avec $n=10^6$) et dans le registre du calcul (le logiciel est incapable de calculer $\int_0^1\left(1+\frac{x}{10^6}\right)^{10^6} dx$^4.13. La bifurcation didactique qui suit fait investir à G1 la situation adidactique de recherche du plus grand entier ne donnant pas une valeur 0 pour l'intégrale de façon à approcher au mieux la limite souhaitée. Le résultat ainsi obtenu ne parle pas à G1 qui conclue cette phase par une interrogation :  La conjecture, je mets quoi ? .

Quatrième épisode : calcul de l'intégrale.

Dans cet épisode, une suite d'incidents mathématiques se succèdent dans l'utilisation des formules habituelles et la confrontation avec les résultats fournis par la machine ; d'abord, G1 n'utilise pas la formule correcte pour la détermination d'une primitive et se perd dans son calcul à la main, ne sachant finalement plus quelle est la variable d'intégration : La primitive, c'est sur $n$ ou sur $x$ ? .

Un incident syntaxique suit alors puisque le résultat fourni par le logiciel est écrit de façon inhabituelle :

$$\frac{(x+n)\left(\frac{x+n}{n}\right)}{n+1}$$

au lieu de :

$$\frac{n}{n+1}\left(1+\frac{x}{n}\right)^{n+1}$$

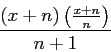
Il faut l'aide de l'examinateur pour avancer dans ce calcul et les changements de registres de représentation du même objet dans le registre de la calculatrice et dans le registre de l'écriture provoquent des erreurs.

Finalement, G1 reprend la syntaxe du logiciel pour expliciter à la main les calculs.

Cinquième épisode : calcul de la limite en 0 de $\frac{\ln(1+x)}{x}$ ; la méthode de calcul de cette limite est connue par G1 qui après quelques hésitations arrive au résultat.

Sixième épisode : le calcul de la limite.

L'incident syntaxique du quatrième épisode a pour conséquence une perturbation qui empêche G1 de faire le lien entre la forme proposée par l'énoncé et son résultat en masquant le changement de variable $m=\frac{1}{n}$ qui fait le lien avec l'indication donnée. La conséquence de cet incident est alors une bifurcation nildidactique qui correspond à l'essai de calcul de la limite utilisant des résultats sur les fonctions rationnelles, inefficaces dans ce cas.