Analyse descendante

La situation noosphérienne (cf. paragraphe milieux) relève ici de la position de Marie dans l'expérimentation. Volontaire pour accepter d'enseigner dans une classe dont tous les élèves sont équipés de la calculatrice, elle accepte de plus l'intrusion d'un chercheur dans sa classe, alors que, de ses propres dires, elle n'est pas à l'aise avec la technologie. Elle sépare très strictement ce qui relève de ce qu'elle considère être les mathématiques (science hypothético-déductive) du travail fait avec les calculatrices ou le logiciel qui apparaît plus comme une motivation que comme un support au raisonnement. Elle prépare cependant assidûment ses élèves à l'épreuve expérimentale de mathématiques. Dans ce cas, la situation S+3 de Marie peut être décrite comme :

P+3 cherche à entrainer ses élèves pour l'épreuve pratique de mathématiques (EPM). Elle souhaite donc que les élèves utilisent dans une situation d'autonomie le logiciel sans pour autant perdre de vue le nécessaire entraînement au programme de mathématiques de Terminale S

La situation de construction prend en compte la contradiction entre la volonté de laisser une autonomie aux élèves et le désir de faire en sorte que les élèves ne passent pas tout le temps de la séance sur le logiciel mais arrive dans l'heure à aborder ce que Marie appelle la partie théorique^4.2.

Dans cette situation S+2, P+2 construit une succession de questions permettant, un peu à la manière d'un tutoriel d'avancer dans la réalisation de la figure pour faire apparaître la conjecture souhaitée et pour permettre aux élèves d'arriver à la question de la démonstration de la conjecture.

La situation de projet met en uvre cette construction en insérant les choix didactiques à la fois concernant la volonté de faire apprendre aux élèves le fonctionnement du logiciel et de mener à bien la résolution du problème mathématique.

La présentation du TP commence par un énoncé de type mathématique introduisant les objets en jeu : deux points $A$ et $B$ donnés par une représentation dans le plan complexe, le cercle trigonométrique C, un point $M$ de ce cercle et l'application de C dans $\Re^+$ qu'il s'agira d'étudier. Cette partie a été photocopiée sur un manuel.

Le titre encadré : réalisation de la figure et conjectures met en jeu à la fois les mathématiques (conjectures) et l'utilisation de l'instrument (réalisation de la figure) ; en revanche, dès la première consigne, le choix de l'outil technique est imposé :

Ouvrir un classeur. Graphiques et géométrie

Les différentes étapes de l'énoncé montrent bien cette alternance entre des explications et des questions mathématiques et des conseils et des constructions avec le logiciel.

Il est également intéressant de noter que le but du TP apparaît seulement au bas de la première page après un ensemble de consignes facilitant la construction de la figure initiale : l'étude des variations de $f$ en fonction de l'angle $\alpha$^4.3 dans un type mathématique suivi d'une remarque de type instrumental sur les capacités du logiciel à  ne mesurer que des angles géométriques, remarque illustrée de deux dessins faisant apparaître dans deux positions du point $M$ la valeur positive en radian de l'angle $\left(\widehat{\stackrel{\rightarrow}{OU},\stackrel{\rightarrow}{OM} }\right)$. 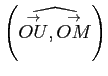Dans le langage mathématique, la différence entre angle géométrique et angle orienté est expliquée pour justifier la manipulation instrumentale demandée et partant du constat que le logiciel ne sait pas gérer les mesures des angles orientés, Marie fait construire la mesure de l'angle orientée à partir du signe de l'ordonnée du point du cercle trigonométrique et de la mesure de l'angle géométrique. Les explications sont d'abord d'ordre mathématique (lorsque $\alpha$ appartient à l'intervalle $]-\pi;\pi]$, les signes de $\frac{\vert y\vert}{y}$ et de $\alpha$ sont les mêmes) puis d'ordre technique : comment faire calculer une formule au logiciel ?

Dans la situation S+1, P+1 choisit d'intégrer les questions mathématiques dans les questions d'ordre technologique.

La situation didactique S0 va mettre en uvre les choix didactiques locaux : permettre un travail en autonomie et un apprentissage des fonctionnalités du logiciel en gardant un contenu mathématique consistant. La façon dont P0 place la situation montre cette double volonté contradictoire d'autonomie et de guidage tutoriel :

Bon, ouvrez l'ordinateur et regardez si ça marche. Allez...(brouhaha) ; le professeur navigue dans la classe, et intervient auprès des élèves :

A tu vas maintenant te mettre là...

Les écrans, ils marchent ou pas ? C'est la séance cinéma aujourd'hui. J. tu te mets à côté d'A...

Ça y est, ça marche. Bon alors on commence à... page 1, 2, 3, 4... Alors vous allumez l'écran, s'il vous plait, rapidement...

Ça marche ou pas ? Oui, ça marche...

Allez !

Donc on commence par la page 1... d'accord ! C'est numéroté page 1, 2, 3, 4...  Allez, c'est parti...  Je vous guide pas mal, là. Ça vous permet de vous réapproprier certains trucs, certains menus.

Bon alors, c'est validé... maintenant pointeur, tu te mets sur les coordonnées... là, voilà, pointeur, coordonnées, vas y ! voilà, non tu sélect... tu... enter, voilà !

L'organisation de la salle de classe et l'attitude de P0, dès l'entrée montre que l'utilisation du logiciel est d'une manière contrainte par les conditions extérieures, et que l'objectif mathématique (théorique dit Marie) est d'une plus grande importance. Dans cette brève introduction, on entend : vous allumez l'écran, s'il vous plait, rapidement, séance cinéma aujourd'hui, je vous guide pas mal, là., réapproprier certains trucs, certains menus ; autant de positions visant à accélérer les manipulations pratiques et dévoilant la position P+3 dans P0.

P0 cherche à faire en sorte que les élèves expérimentent la syntaxe du logiciel avant de rapidement les mener vers une construction théorique

La position dans la situation S-1 du professeur est alors toute tracée : P-1 cherche à faire construire et expérimenter sur le logiciel dans les cadres exacts fixés par les questions du TP. La première partie est alors en dehors du contexte de l'apprentissage des mathématiques, ce qui explique que les interactions avec les élèves se situent dans le domaine technique.

De ce fait, P-1 observe les élèves de manière à ce qu'ils avancent ensembles dans la partie expérimentale du TP.

Les allers-retours entre les positions S+3 (nécessité de laisser une autonomie aux élèves) et S-1 (volonté de faire avancer conjointement la classe) contraignent Marie à des interventions difficilement compréhensibles par les élèves et provocatrices d'incidents didactiques.