Analyse mathématique du problème

Le problème consiste à déterminer le minimum et le maximum d'une fonction définie à partir d'une situation géométrique :

Dans un repère orthonormal direct, on considère les points $A$, $B$ d'affixes $z_A=1+i$ et $z_B=-\frac{1}{2}+\frac{1}{2}i$. On appelle C le cercle de centre $O$ et de rayon 1.

1. Donner la forme exponentielle de $z_A$ et de $z_B$.
2. On considère le point $M$ d'affixe $e^{i\alpha}$ avec $\alpha \in ]-\pi,\pi]$. Justifier que $M$ appartient au cercle C.

   On considère l'application $f$ qui à tout point $M$ de C associe $f(M)=MA \times MB$.

3. Montrer que pour tout $\alpha$ de R, l'égalité :
   
   $$e^{i2\alpha}-1=2i\sin \alpha e^{i\alpha}$$
   
   

   Montrer l'égalité :
   

   $$f(M)=\sqrt{\frac{1}{4}+\left(-\frac{3}{2}+2\sin \alpha\right)^2}$$
   
   
   1. En utilisant les résultats précédents, montrer qu'il existe deux points $M$ de C, dont on précisera les coordonnées, pour lesquels $f(M)$ soit minimal. Donner cette valeur minimale.
   2. Montrer qu'il existe une unique point $M$ de C, dont on donnera les coordonnées, pour lesquels $f(M)$ soit maximal. Donner cette valeur maximale.

Voir l'énoncé distribué aux élèves en figure enonce15janv dont le titre est  Optimisation et complexes .

Figure: Enoncé du TP en salle informatique du 15 janvier, page 1

Figure: Enoncé du TP en salle informatique du 15 janvier, page 2

Figure: Enoncé du TP en salle informatique du 15 janvier, page 3

Figure: Enoncé du TP en salle informatique du 15 janvier, page 4

Le problème proposé est un problème d'optimisation qui repose sur la définition et l'étude d'une fonction de R dans R⁺ définie comme le produit des distances d'un point $M$ appartenant au cercle trigonométrique et de deux points $A$ et $B$ fixés. La première partie du TP consiste à  expérimenter sur l'application de géométrie dynamique, de récupérer dans le tableur les valeurs obtenues et de représenter le nuage de points pour faire apparaître les variations de la fonction. La dernière partie, appelée, partie théorique, consiste à  déterminer la forme analytique de cette fonction et de l'étudier,  à  la main .

L'énoncé est construit en séparant une expérience sur la représentation graphique de la fonction avant sa détermination analytique. Le recours aux nombres complexes apparaît de plus comme un artifice non nécessaire, le point $M$ pouvant être considéré comme le point de coordonnées $(\cos \alpha, \sin \alpha)$. Dans ces conditions le logiciel utilisé donne comme expression de la fonction $f$ en calculant $MA^2\times MB^2$ et en prenant la racine carrée :

$$f(\alpha)=\sqrt{\frac{8\sin^2 \alpha -12 \sin \alpha +5}{2}}$$

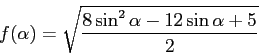
Le logiciel calcule la dérivée de cette fonction et affiche :

$$\frac{(4\sin \alpha-3)\cos \alpha . \sqrt{2}}{\sqrt{8\sin^2 \alpha -12 \sin \alpha +5}}$$

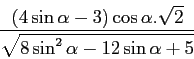
Le dénominateur étant à l'évidence positif et le numérateur factorisé, la détermination des variations de la fonction peut être faite par un élève de terminale. Une difficulté pouvant être la mise en relation de l'expression trouvée par cette méthode et le résultat annoncé dans l'énoncé puisque l'opération de factorisation partielle qu'elle représente n'est pas naturelle. Dans ce cas, le développement du résultat permet de montrer facilement l'égalité, mais cette opération n'est certainement pas naturalisée en terminale. Tout comme dans le devoir à la maison, résoudre le problème avec la calculatrice impose bien sûr, une connaissance de son fonctionnement et de ses possibilités mais surtout un recul vis-à-vis du calcul algébrique à mener. L'introduction artificielle des nombres complexes ne simplifie pas les calculs.

Dans la première partie, l'énoncé propose une construction géométrique et un tracé du nuage de points lorsque le point $M$ fait un tour complet sur le cercle. Bien entendu, le phénomène est périodique et la période est a priori inférieure ou égale à $2\pi$ (ici, exactement $2\pi$). Le choix de l'intervalle dans lequel on va étudier cette fonction relève ici d'un argument lié au fonctionnement du logiciel qui permet de mesurer les angles géométriques rentrants dont les mesures sont comprises entre 0 et $\pi$ radians. Cette remarque permet de prévoir dans le cours du TP une difficulté, potentiellement génératrice d'incident, d'autant plus que l'énoncé demande de travailler dans l'intervalle $[-\pi,\pi[$ sans justifier ce choix^4.1.

La construction du nuage de points permet une visualisation de la courbe de la fonction sans la définir analytiquement mais aussi sans qu'il soit possible, sans aide, de  reconnaître  la fonction. De ce fait, la distance entre les expériences et le calcul semble très importante. Même dans l'application  Données & statistiques  du logiciel, les régressions proposées ne permettent pas d'approcher la définition analytique de la fonction.

Une régression sinusoïdale qui pourrait sembler pertinente n'aboutit pas ce qui se comprend puisque la régression sinusoïdale du logiciel est de la forme $a\sin(x+b)+c$. En revanche, il est possible et naturel de chercher une fonction du second degré en sinus et de définir une fonction $g$ de la forme $g(x)=a\sin^2 x+b\sin x+c$ et faire varier les coefficients $a$, $b$ et $c$ de façon à s'approcher du nuage de points du produit des carrés des distances puis de la racine carrée comme illustré sur la figure regression. Cette étude permet de faire le lien entre l'expérience géométrique et l'analyse du problème, mais elle est absente de l'énoncé du problème ce qui ne fait que renforcer la séparation entre l'analyse (appelée partie théorique) et l'expérience géométrique.

Figure: Régression sinusoïdale quadratique

Les objets mathématiques en jeu et leurs représentations sont reliés fondamentalement mais l'énoncé ne permet pas d'établir tous les liens.

Dans ce problème, les objets mathématiques de base sont le cercle, la distance de points du plan, les variations de grandeurs. Chacun de ces objets est représenté de différentes façons utilisant des registres de représentations différents :

Objet	Graphique	Numérique	Algébrique	Analytique
Cercle	Dessin papier Dessin numérique		Trigonométrie (appel aux définitions des lignes trigonométriques) nombres complexes (appel aux différentes représentations) argument (lien avec les angles orientés)	Appel aux fonctions trigonométriques
Distance entre deux points	Mesure (règle ou outil de mesure)	Calcul posé Calcul machine (utilise un outil)	Distance euclidienne. Module d'un complexe	fonctions racine et carré
Variation	Dessin dynamique	Tableur Affichage numérique		Appel à d'autres objets : dérivée, signe qui renvoient sur de nouvelles représentations

Les conversions entre les représentations des objets sont implicites et ne sont pas tous pris en charge dans l'énoncé. Les conversions entre les registres graphiques, numériques et algébriques ne vont que dans le sens Graphique $\leftarrow$ Numérique $\rightarrow$ Algébrique et les conversions à des registres de représentations du cadre de l'analyse et les retours ne sont pas utilisés. Dans l'énoncé, le retour du calcul vers l'expérience n'est pas envisagé ; on peut imaginer qu'il n'est pas naturel et qu'il aura pour conséquence une séparation des cadres dans lesquels les expériences vivent et des cadres de résolution du problème.