suivant: Analyse descendante monter: Première matinée d'observation (15 précédent: TD en salle de Table des matières
La solution guidée par l'énoncé conduit à un calcul sur les nombres complexes utilisant l'écriture complexe de la rotation. Ainsi :
Et les milieux ![]() ,
, ![]() et
et ![]() ont pour affixes respectives :
ont pour affixes respectives :
et dans ces conditions :
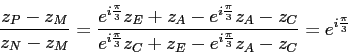
ce qui permet de conclure : le triangle ![]() est équilatéral car isocèle et d'angle au sommet
est équilatéral car isocèle et d'angle au sommet ![]() .
.
Cette solution est calculatoire et rapide mais ne permet pas de comprendre le phénomène géométrique en jeu.
Une démonstration géométrique
Une démonstration géométrique repose sur le lemme suivant :
Lemme : Soit ![]() un parallélogramme et
un parallélogramme et ![]() et
et ![]() les triangles équilatéraux directs construits sur les côtés du parallélogramme. (Voir figure lemme). Alors,
les triangles équilatéraux directs construits sur les côtés du parallélogramme. (Voir figure lemme). Alors, ![]() est un triangle équilatéral.
est un triangle équilatéral.
Si on considère les triangles ![]() et
et ![]() : les côtés
: les côtés ![]() et
et ![]() sont de même longueur puisque
sont de même longueur puisque ![]() est un parallélogramme. Les côtés
est un parallélogramme. Les côtés ![]() et
et ![]() sont aussi de même longueur, puisque les côtés d'un triangle équilatéral.
sont aussi de même longueur, puisque les côtés d'un triangle équilatéral.
Par ailleurs, si on considère la rotation vectorielle d'angle ![]() l'image du vecteur
l'image du vecteur
![]() est le vecteur
est le vecteur
![]() et du vecteur
et du vecteur
![]() est
est
![]() ; par conséquent les angles de vecteurs
; par conséquent les angles de vecteurs
![]() et
et
![]() sont égaux. Par conséquent les angles géométriques
sont égaux. Par conséquent les angles géométriques ![]() et
et ![]() sont de même mesure. Les triangles
sont de même mesure. Les triangles ![]() et
et ![]() sont isométriques et finalement les angles
sont isométriques et finalement les angles
![]() et
et ![]() ont même mesure et
ont même mesure et ![]() .
.
On en déduit alors que ![]() vaut
vaut ![]() et par conséquent que le triangle
et par conséquent que le triangle ![]() est équilatéral.
est équilatéral.
Utilisons alors ce lemme dans le problème. J'appelle ![]() ,
, ![]() et
et ![]() les symétriques de
les symétriques de ![]() par rapport à
par rapport à ![]() ,
, ![]() et
et ![]() .
.
Comme illustré sur la figure dem1, et comme ![]() est un parallélogramme,
est un parallélogramme, ![]() et
et ![]() sont des triangles équilatéraux construits sur deux côtés consécutifs de ce parallélogramme, par application du lemme, le triangle
sont des triangles équilatéraux construits sur deux côtés consécutifs de ce parallélogramme, par application du lemme, le triangle ![]() est équilatéral. En particulier, l'angle
est équilatéral. En particulier, l'angle
![]()
Considérons alors les triangles ![]() et
et ![]() (Figure dem2),
(Figure dem2),
On en déduit que les triangles ![]() et
et ![]() sont isométriques et donc que les angles
sont isométriques et donc que les angles
![]() et
et
![]() sont de même mesure ; par conséquent
sont de même mesure ; par conséquent
On en déduit alors que ![]() est équilatéral.
est équilatéral.
En utilisant alors l'homothétie de centre ![]() et de rapport
et de rapport ![]() , l'image de ce triangle est le triangle
, l'image de ce triangle est le triangle ![]() qui est donc, lui aussi équilatéral.
qui est donc, lui aussi équilatéral.
Cette démonstration géométrique, bien que n'utilisant que des objets mathématiques connus en terminale n'est cependant pas simple et demande une analyse fine de la figure de géométrie. Il est d'ailleurs remarquable que la démonstration utilisant les nombres complexes soit si simple et rapide, alors que les arguments géométriques sont, quant à eux, délicats à mettre en évidence. C'est bien sûr l'intérêt de cet exercice qui montre la puissance de l'outil des nombres complexes et une difficulté, puisque l'on ne peut comprendre cet intérêt sans s'être heurté à la démonstration géométrique. L'expérience géométrique qui consiste à représenter la situation dans un logiciel de géométrie dynamique ne peut ainsi pas être mis en relation avec le raisonnement algébrique proposé, ce qui ne fait qu'accentuer le fossé existant entre l'expérience et le raisonnement, déjà mis en évidence dans la situation précédente.
Gilles 2012-03-05