Approche épistémologique

Les phénomènes scientifiques ne peuvent être inclus dans un dispositif expérimental que dans la mesure où ils sont qualifiés comme objet ; les mathématiques n'échappent pas à cette réflexion et les rapports entre la réalité et les objets mathématiques doivent être précisés. Dans une perspective platonicienne, les mathématiques existent en-soi et les mathématiciens les découvrent et les explorent comme un explorateur découvre un nouveau continent. A l'opposé, la position kantienne propose les mathématiques comme une construction humaine qui doit déterminer et définir ses objets a priori.

En mathématiques, par exemple, définir un objet consiste bien essentiellement à l'introduire explicitement dans un système opératoire, que ce soit en donnant une procédure de construction, ou que ce soit en formulant des énoncés et des règles où entre le nom de l'objet à définir. En ce dernier cas, qui est celui de l'axiomatisation, l'objet se trouve médiatement défini, en ce sens que l'on a les moyens de manipuler et combiner tous les énoncés bien construits où entre son nom. [page 195]Granger2003

Les différents niveaux de réalité proposés par Kant1905 permettent de modéliser le réel et de considérer les objets mathématiques comme élément de ce modèle :

• réalité sensible : ce qui est perçu par nos sens ou par un instrument construit ;
• réalité empirique : que l'on peut soumettre à l'expérience, l'expérience étant dans ce cas considérée comme une somme d'observations dont on peut tirer des corrélations, par conséquent extérieur au concept de temps et au concept de causalité ;
• réalité objective (ou objectivée) : sur laquelle on va pouvoir construire des expériences via une modélisation mathématique. Au delà de l'observation, il s'agit plus d'une réflexion à travers une modélisation mathématique des résultats de l'observation. C'est de fait lié à la causalité et au temps ;
• réalité en soi (terminologie de Kant) ou plus récemment, réalité inaccessible :

  Mais la vérité du résultat auquel nous arrivons dans cette première application de notre connaissance rationnelle a priori nous est fournie par la contre-épreuve de l'expérimentation, en cela même que cette faculté n'atteint que des phénomènes et non les choses en soi qui, bien que réelles par elles-mêmes, restent inconnues de nous. [page 24, préface de la seconde édition]Kant1905.

L'expérience ne prend en considération que les réalités sensibles, empiriques et objectives. La réalité en soi échappe à l'expérience, et même, d'une façon plus radicale, la réalité en soi est contradictoire avec l'expérience. Ce que l'on peut alors appeler expérience en mathématiques, c'est un travail sur des représentations naturalisées des objets mathématiques définis dans un système de signes. Le terme naturalisé   étant à prendre au sens de la maîtrise des transformations internes à un registre de représentation sémiotique d'un objet ou des conversions d'un registre dans l'autre Duval1996. L' expérience  ayant alors comme objet de délimiter ou d'explorer les propriétés de l'objet en lien avec une théorie :

Ce qui caractérise la dimension expérimentale en mathématiques, c'est le va-et-vient entre un travail avec les objets que l'on essaye de définir et de délimiter et l'élaboration et/ou la mise à l'épreuve d'une théorie, le plus souvent locale, visant à rendre compte des propriétés de ces objets.[page 1]Exprime2010b

Ainsi, les concepts mathématiques bien que produits dans l'esprit n'ont de sens que dans leurs relations avec les phénomènes empiriques :

Aussi est-il indispensable de rendre sensible un concept abstrait, c'est-à-dire de montrer dans l'intuition un objet qui lui corresponde, parce que sans cela le concept n'aurait, comme on dit, aucun sens, c'est-à-dire aucune valeur. [page 253]Kant1905

La modélisation proposée par [page 100]Mizony2006 est schématisée ci-dessous :

Schéma de modélisation

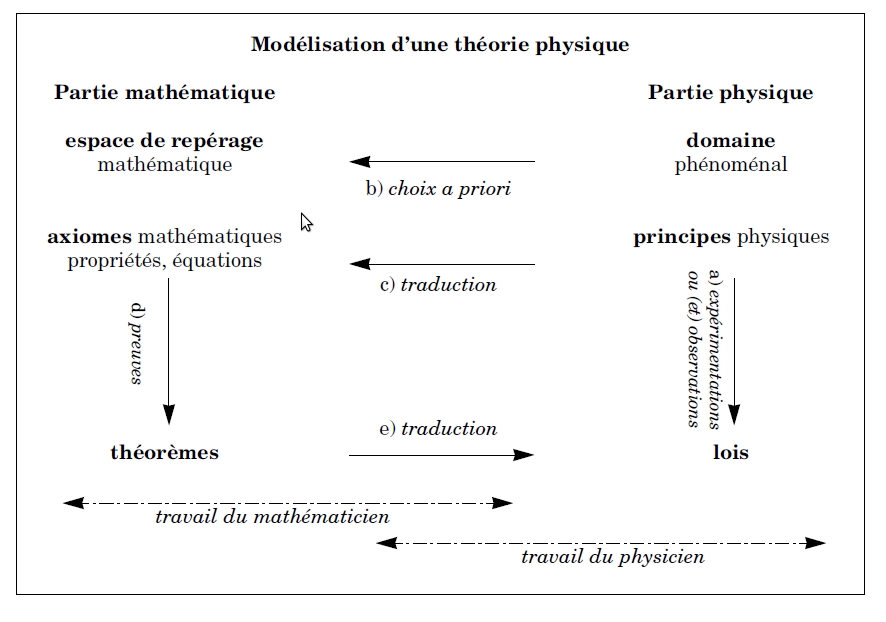
Les positions relatives des mathématiques et de la physique peuvent être illustrées avec la théorie de la relativité restreinte. Cette théorie repose sur la constance de la vitesse de la lumière. Ce fait  repose sur notamment les expériences de Fizeau en 1849 puis Michelson en 1878. Les expériences sont décrites et objectivées  en utilisant le temps de l'observateur. Sous ces hypothèses la mécanique classique est mise en défaut puisque ce résultat est en contradiction avec les compositions des vitesses. En 1905, quasi simultanément, Poincaré utilisant une méthode de physicien (minimisation de l'énergie via un Laplacien) et Einstein utilisant une méthode de mathématicien (définition de la métrique $d^2=x^2+y^2+z^2-t^2$ dans l'espace temps à quatre dimensions) proposent une modélisation reposant sur la vitesse constante de la lumière. Dans le schéma, on fait le parcours :

• domaine phénoménale ($c=Cste$),
• espace de repérage mathématique : écriture des équations sous ces hypothèses,
• traitement mathématiques,
• traduction dans les lois physiques.

Ces considérations philosophiques sur la nature des objets sont d'une grande importance pour leur enseignement ; en effet, et en particulier dans un environnement informatique, la place de l'expérience sur les objets mathématiques semble être une hypothèse largement partagée. Or, les expériences sont construites non pas sur les objets de nature fondamentalement synthétiques mais sur des représentations de ces objets qui permettent d'étendre et de développer le concept pour le rendre intelligible (pour reprendre la terminologie de Kant). L'expérience,  liaison synthétique des intuition  [page 47]Kant1905, permet à la fois de construire des connaissances nouvelles et de faire fonctionner des connaissances anciennes et naturalisées. La nature même de l'expérience mathématique porte donc en soi l'éventualité de bifurcation didactique.

Les dialectiques artefact-instrument et ressource-document proposées dans les approches instrumentales et documentaires sont alors à mettre en relation avec les objets et leurs représentations. Tout comme la ressource se transforme en document en lui associant, dans un contexte particulier, des schèmes d'utilisation, l'objet se construit par les expériences réalisées sur certaines de ses représentations.

La compréhension de certains objets mathématiques et la possibilité de leurs représentations sont étroitement liées. Et pour reprendre les propos précédents, un est différent de 1. Il s'agit donc de représenter les objets mathématiques dans des registres de représentation sémiotique différents, et comprendre un objet mathématique nécessite d'appréhender ses représentations dans des registres variés.