Observation : G1 - classe de Marie

Je désignerai par G1, l'élève observé. Le sujet tiré au hasard est le sujet 121, Limites d'intégrales  dont le but est de déterminer la limite lorsque $n$ tend vers l'infini de la suite d'intégrales définies par :

$$I_n=\int_0^1\left(1+\frac{x}{n}\right)^n dx$$

Sujet 121

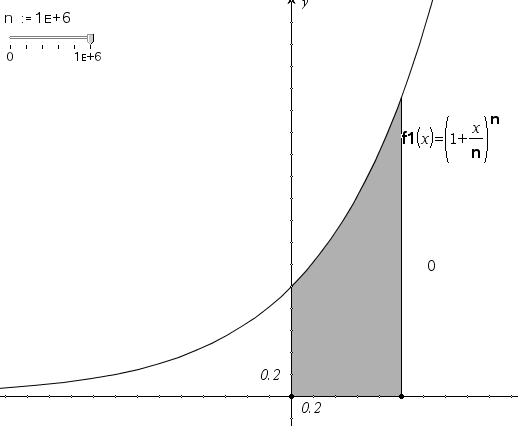
9h30 Dès son arrivée devant l'ordinateur, G1 ouvre une session à  son nom et lance le logiciel. Il lit le sujet. Il ouvre une page graphique et entre :

$$f_1(x)=\left(1+\frac{x}{n}\right)^n$$

G1 parcourt les menus. Très rapidement, s'arrête sur le menu de la figure 1. Il place le curseur sur la page graphique, écrit $n$ pour la variable du curseur, avec le bouton droit de la souris, il fait apparaître les propriétés du curseur. Il modifie les axes de coordonnées. Il modifie nmax en 1000, puis en 1 000 000. Il bouge le curseur et regarde la courbe à  l'écran.

Figure 1

9h37 : Il s'arrête pour lire le sujet et réfléchir. Il n'écrit rien.

9h40 : Intervention du professeur : Bon, tu as fait le 1 et le 2. Est-ce que tu peux me dire quelle est l'allure de la courbe ?

G1 : Ça ressemble à  l'exponentielle 

P : Tout à  fait. Ecrit ça sur ta copie . P s'éloigne.

G1 prend un stylo et écrit sur la copie : Quand $n$ devient très grand, $f_n$ ressemble à  la fonction exponentielle

9h41 : G1 prend une feuille de brouillon. Il ferme son stylo. Il ouvre une page calcul, tape fn, efface, tape fn=, efface, fn(x)= efface tout. Il revient sur l'écran graphique.

9h44 : Il parcourt les menus, trouve le menu intégrale (figure 2)

Figure 2

9h45 : P passe ; Tu en es à  la question 3 ? Est-ce que tu penses que c'est séparé ? Géométriquement, c'est quoi une intégrale ? 

G1 une aire . Il revient sur la page graphique.

P : trace le 

G1 hésite... utilise le menu Mesure, Intégrale de l'application Graphiques & géométrie. (figure 3) ; P s'éloigne. Il sélectionne la courbe, le point d'intersection des axes, le point de coordonnées (0,1). L'affichage indique 0 (figure 4). Il revient en arrière en utilisant Ctrl Z.

Figure 3 Figure 4

P : Qu'est ce que tu cherches à  faire ? 

G1 : A mesurer l'aire 

P : Est-ce que le logiciel te permet de le faire ?  P sélectionne le menu puis refait les manipulations.

G1 : C'est ce que j'avais fait...  Il revient en arrière avec Ctrl Z.

P fait refaire la manipulation à  l'élève. L'affichage est toujours 0. P : Il y a un truc que je ne comprends pas... . Il voit la valeur $10^6$ de $n$. Il faut être raisonnable...  ; il modifie cette valeur en $10^2$. L'aire s'affiche. P : Pourquoi, ça ne marche pas, je suis incapable de te le dire... . Il s'éloigne.

G1 modifie les valeurs de nmax ; il s'aperçoit qu'à  partir de $3,9\times 10^2$^6.4, l'aire affichée devient nulle. Il essaye, plusieurs fois pour 380, 390, il modifie la visualisation du curseur...

G1 : appelle P : La conjecture je mets quoi ? Ça ?  Il montre la valeur obtenue à  l'écran.

P : Oui . G1 écrit sur la feuille : Graphiquement les valeurs de $I_n$ se rapprochent de 1,79176.

Il écrit Partie B.

Directement sur sa feuille :

$f_n(x)=\left(1+\frac{x}{n}\right)^n$ de la forme $(u)^n$

de primitive $\frac{n}{(n+1)}(u)^{n+1}$

donc $F_n(x)=\frac{n}{(n+1)}\times\left(1+\frac{x}{n}\right)^{n+1}$

$$=\frac{n}{(n+1)}\times\left(1+\frac{x}{n}\right)^{n}\times(1+\frac{x}{n})$$

$$=\left(\frac{n}{n+1}+\frac{x}{n+1}\right)\times\left(1+\frac{x}{n}\right)^n=\frac{(x+n)\times(1+\frac{x}{n})^n}{(n+1)}$$

9h59 Il lève le doigt ; P s'approche. G1 : La primitive, c'est sur $n$ ou sur $x$ ? .

P : Dérive moi ça... Quand tu dérives, ça, ...  Il rajoute sur la copie u' de la forme $u'(u)^n$.

P : Il y avait quelque chose de facile dans la partie calcul ; il demande à  G1 de se placer sur sa feuille calcul.  Tu mets $p$ à  la place de $n$, parce que $n$ c'est déjà  défini . G1 fait effectuer le calcul de la figure 5 :

Figure 5

P passe : Si t'es bloqué, rien ne t'empêche de faire sur la machine .

P montre le résultat : Là , tu as $\left(1+x\right)^{p+1}$, tu vois... Si tu es bloqué sur la primitive, la machine te la donne. . P montre sur papier :

$$\mbox{avec } u=1+\frac{x}{n} \mbox{ donc } u'=1+\frac{1}{n}=\frac{n+1}{n}$$

$$u'u^n \mbox{ a pr pr..} \frac{u^{n+1}}{n+1}$$

$$\frac{n+1}{n}\times\left(1+\frac{x}{n}\right)^n \dots \frac{1}{n+1}\left(1+\frac{x}{n}\right)^{n+1}$$

$$\left(1+\frac{x}{n}\right)^n \dots \frac{n}{(n+1)^{2}}\left(1+\frac{x}{n}\right)^{n+1}$$

il s'aperçoit de son erreur, il écrit au dos de l'énoncé :

$$\frac{1}{n+1}(u)^{n+1}=\frac{n+1}{n+1}\times (u)^n \times u'$$

$$=(u)^n\times\frac{1}{n}$$

G1 remarque et lui indique l'erreur, P rectifie ...

$$\mbox{avec } u=\mbox{\xout{1+}}\frac{x}{n} \mbox{ donc } u'=1+\frac{1}{n}=\frac{\mbox{\xout{n+1}}}{\mbox{\xout{n}}} \frac{1}{n}$$

$$u'u^n \mbox{ a pr pr..} \frac{u^{n+1}}{n+1}$$

$$\frac{1}{n} \frac{\mbox{\xout{n+1}}}{\mbox{\xout{n}}} \times\... ...n}\right)^n \dots \frac{1}{n+1}\left(1+\frac{x}{n}\right)^{n+1}$$

$$\left(1+\frac{x}{n}\right)^n \dots \frac{n}{(n+1)^{\mbox{\xout{2}}}} \left(1+\frac{x}{n}\right)^{n+1}$$

puis donne des conseils sur le bac.

G1 reprend les calculs en intégrant par parties.

Sur la copie, on peut lire :

Donc

$$I_n=\int_0^1\left(1+\frac{x}{n}\right)^n dx$$

$$\left[F_n(x)\right]_0^1$$

$$=\left[(x+n)\times \left(1+\frac{x}{n}\right)^n \times\frac{1}{n+1}\right]_0^1$$

$$=(1+n)\times\left(1+{1\over n}\right)^n\times{1\over n+1}-n\times(1)^n\times{1 \over n+1}$$

$$=\frac{(1+n)\times\left(1+{1\over n}\right)^n-n}{(n+1)}$$

$$=\left(1+{1\over n}\right)^n-{n \over n+1}$$

10h07 G1 obtient le résultat de la question 3 et s'attaque au problème de la limite indiqué sur l'énoncé :

$$\lim_{n\to 0}\frac{\ln (1+x)}{x}=1$$

Il écrit^6.5 :

5) Nombre dérivé de ln(1x) en

Taux d'accroissement : $\left( \ln(1)\right)'= \hskip -9pt \lim\limits_{h \to 0} \frac{\ln(1+h)-\ln(1)}{h}$

= $\lim\limits_{h \to 0} \frac{\ln(1+h)}{x \hskip -4pt h}$

Or $(\ln(x))'={1 \over x}$ donc $(\ln((1))'=1$

On a $\lim\limits_{x \to 0}\frac{\ln(1+x)}{x}=$

Il réfléchit sans rien écrire...

puis, il écrit :

$$\lim_{n \to +\infty}I_n=\lim_{n \to +\infty} \left(1+{1 \over n}\right)^n-\left(1+{1 \over n}\right)$$

=0

car $\lim\limits_{n \to + \infty} \left(1+{1 \over n}\right)=$01

et $\lim\limits_{n \to + \infty}\left(1+{1 \over n}\right)^n= 1$

et $\lim\limits_{n \to + \infty} -\left(1+{1 \over n}\right)= -1$

Le professeur ramasse les copies.

Fin de la séance.